第三章数据价值的度量

从数据资产的角度来看，数据价值的度量是数据资产定价的核心问题。

3.1 度量的基本概念

在数学中，度量（Metric）是一个函数，用于定义集合中元素之间的距离。度量满足以下三个条件：

非负性（Non-negativity）：对于任意两个元素 $x$ 和 $y$ ，度量 $d (x, y)$ 总是非负的，即 $d (x, y) \geq 0$ ，并且当且仅当 $x = y$ 时， $d (x, y) = 0$ 。
对称性（Symmetry）：对于任意两个元素 $x$ 和 $y$ ，度量 $d (x, y)$ 满足对称性，即 $d (x, y) = d (y, x)$ 。
三角不等式（Triangle Inequality）：对于任意三个元素 $x$ 、 $y$ 和 $z$ ，度量 $d (x, y)$ 满足三角不等式，即 $d (x, z) \leq d (x, y) + d (y, z)$ 。

满足上述条件的函数 $d : X \times X \to R$ 被称为度量，其中 $X$ 是一个集合。度量空间（Metric Space）是指一个集合 $X$ 连同其上的度量 $d$ 组成的二元组 $(X, d)$ 。

常见的数学度量

欧式距离（Euclidean Distance）：
- 欧式距离是最常见的度量，用于计算两个点之间的直线距离。对于两个点 $x = (x_{1}, x_{2}, \dots, x_{n})$ 和 $y = (y_{1}, y_{2}, \dots, y_{n})$ ，欧式距离定义为： $d (x, y) = i = 1 \sum n (x_{i} - y_{i})^{2}$
曼哈顿距离（Manhattan Distance）：
- 曼哈顿距离也称为城市街区距离，用于计算两个点之间的路径距离。对于两个点 $x = (x_{1}, x_{2}, \dots, x_{n})$ 和 $y = (y_{1}, y_{2}, \dots, y_{n})$ ，曼哈顿距离定义为： $d (x, y) = i = 1 \sum n ∣ x_{i} - y_{i} ∣$
切比雪夫距离（Chebyshev Distance）：
- 切比雪夫距离用于计算两个点之间的最大坐标差。对于两个点 $x = (x_{1}, x_{2}, \dots, x_{n})$ 和 $y = (y_{1}, y_{2}, \dots, y_{n})$ ，切比雪夫距离定义为： $d (x, y) = i max ∣ x_{i} - y_{i} ∣$
余弦相似度（Cosine Similarity）：
- 余弦相似度用于衡量两个向量之间的相似性。对于两个向量 $x$ 和 $y$ ，余弦相似度定义为： $cosine_similarity (x, y) = \frac{x \cdot y}{∥ x ∥∥ y ∥}$ 其中， $x \cdot y$ 表示向量的点积， $∥ x ∥$ 和 $∥ y ∥$ 表示向量的范数。
马氏距离（Mahalanobis Distance）：
- 马氏距离用于衡量数据点与数据集中心之间的距离，考虑了数据的协方差。对于��据点 $x$ 和 $y$ ，马氏距离定义为： $d (x, y) = (x - y)^{T} S^{- 1} (x - y)$ 其中， $S$ 是数据的协方差矩阵。
汉明距离（Hamming Distance）：
- 汉明距离用于计算两个等长字符串之间不同字符的个数。对于两个字符串 $x$ 和 $y$ ，汉明距离定义为： $d (x, y) = i = 1 \sum n δ (x_{i}, y_{i})$ 其中， $δ (x_{i}, y_{i})$ 当 $x_{i} \neq = y_{i}$ 时为1，否则为0。
黎曼度量（Riemannian Metric）：
- 设 $M$ 是一个流形， $g$ 是定义在 $M$ 上的度量张量，对于流形上的两个切向量 $u$ 和 $v$ ，黎曼度量定义为： $g (u, v) = i, j \sum g_{ij} u^{i} v^{j}$ 其中， $g_{ij}$ 是度量张量的分量。
- 需要明确的是，“黎曼度量”是局部的内积结构，通过测地线才能诱导全局意义上的距离函数。即，要获得流形上的距离，需要沿测地线积分黎曼度量，才能得到测地距离。
贝蒂数（Betti Numbers）：
- 贝蒂数用于度量拓扑空间的同调特征。第 $k$ 个贝蒂数 $β_{k}$ 表示拓扑空间中 $k$ 维孔洞的数量。贝蒂数可以通过计算持续同调群得到。

度量学习（Metric Learning）

除了上述可以用数学公式直接表示的度量，还有许多复杂的度量只能通过度量学习（Metric Learning）来找到。度量学习是一种机器学习方法，旨在从数据中学习一个合适的度量函数，使得在该度量下，相似的数据点距离更近，不相似的数据点距离更远。度量学习在图像识别、自然语言处理和推荐系统等领域有广泛的应用。

度量学习的基本概念：
- 度量学习的目标是学习一个映射函数 $f : X \to Y$ ，其中 $X$ 是输入空间， $Y$ 是特征空间。在特征空间中，定义一个度量函数 $d : Y \times Y \to R$ ，使得对于相似的样本对 $(x_{i}, x_{j})$ ， $d (f (x_{i}), f (x_{j}))$ 较小；对于不相似的样本对 $(x_{i}, x_{k})$ ， $d (f (x_{i}), f (x_{k}))$ 较大。
常见的度量学习方法：
- 有监督度量学习：利用带标签的数据进行度量学习。常见的方法包括：
  - 大边界最近邻（Large Margin Nearest Neighbor, LMNN）：通过优化目标函数，使得相似样本对的距离尽可能小，不相似样本对的距离尽可能大。
  - 对比损失（Contrastive Loss）：通过最小化相似样本对的距离和最大化不相似样本对的距离来学习度量函数。
  - 三元组损失（Triplet Loss）：通过最小化三元组 $(an c h or, p os i t i v e, n e g a t i v e)$ 中锚点和正样本的距离，最大化锚点和负样本的距离来学习度量函数。
- 无监督度量学习：利用无标签的数据进行度量学习。常见的方法包括：
  - 自编码器（Autoencoder）：通过将数据编码到低维空间，并在低维空间中定义度量函数。
  - 生成对抗网络（Generative Adversarial Network, GAN）：通过生成器和判别器的对抗训练，学习数据的潜在表示和度量函数。
度量学习的应用：
- 图像识别：在图像识别任务中，度量学习可以用于学习图像的特征表示，使得相似的图像在特征空间中距离更近，从而提高识别准确率。
- 自然语言处理：在自然语言处理任务中，度量学习可以用于学习文本的嵌入表示，使得相似的文本在嵌入空间中距离更近，从而提高文本分类和检索的效果。
- 推荐系统：在推荐系统中，度量学习可以用于学习用户和物品的表示，使得相似的用户和物品在特征空间中距离更近，从而提高推荐的准确性。
度量学习的挑战：
- 数据标注：有监督度量学习需要大量的标注数据，而标注数据的获取成本较高。
- 模型复杂度：度量学习模型通常较为复杂，需要大量的计算资源和时间进行训练。
- 泛化能力：度量学习模型在训练数据上��表现不一定能很好地泛化到测试数据，需要进行模型选择和正则化。

数据集价值与度量的关系

在数据分析和机器学习中，度量是用于衡量数据点之间相似性或差异性的工具。度量的选择直接影响到数据集的分析结果和价值评估。如果一个数据集没有找到任何合适的度量，那么其价值也就无法定义。这一现象可以通过以下数学原理来解释：

度量空间的定义：
- 在数学中，度量空间 $(X, d)$ 是一个集合 $X$ 和一个度量函数 $d : X \times X \to R$ 的组合。度量函数 $d$ 满足非负性、对称性和三角不等式等性质。度量空间为数据分析提供了一个框架，使得我们可以在集合 $X$ 中定义距离和相似性。
度量的存在性与数据结构：
- 度量的存在性依赖于数据集的内在结构。如果数据集没有找到合适的度量，意味着我们无法在数据点之间定义合理的距离或相似性。这将导致数据集在度量空间中无法表示，从而无法进行进一步的数学分析和处理。
度量与数据价值的关系：
- 数据价值的量化依赖于度量函数。例如，信息熵、流形复杂度和拓扑特征等数据价值的度量方法都需要基于特��度量函数。如果没有合适的度量函数，这些方法将无法应用，数据的价值也就无法量化。
度量的选择与数据分析：
- 在数据分析中，度量的选择直接影响到聚类、分类和回归等任务的结果。如果没有合适的度量函数，我们将无法有效地进行数据分析，导致数据的潜在价值无法挖掘和利用。
度量的不可定义性与数据的无序性：
- 如果一个数据集没有找到任何合适的度量，可能意味着数据集是无序的或随机的。在这种情况下，数据点之间没有明确的关系或模式，导致数据集无法在度量空间中表示，其价值也就无法定义。

因此，度量在数据分析和价值评估中起着至关重要的作用。如果一个数据集没有找到任何合适的度量，那么其价值也就无法定义。这一现象反映了度量在量化数据价值中的基础性作用，以及度量空间在数据分析中的重要性。

有时，我们并非找不到度量，而是尚未找到“最能反映业务需求或目标函数”的度量；与此同时，数据在不同上下文和任务需求下可能采用不同度量(乃至核函数、相似度函数)。因此，在具体实践中，我们通常认为，一个数据集如果无法与任何任务目标相匹配或无法定义合理的相似性准则，则难以在该任务中实现价值量化。

度量在量化数据价值和信息价值中的作用

度量在量化数据价值和信息价值中起着至关重要的作用。通过定义适当的度量函数，我们可以将抽象的数据和信息价值具体化，便于分析和比较。以下是度量在量化数据价值和信息价值中的几个关键作用：

量化确定性：
- 信息熵是度量数据集不确定性的重要工具。通过计算数据集的熵值，我们可以量化数据中包含的信息量。信息熵越高，数据的不确定性越大，包含的信息量也越多。反之，信息熵越低，数据的不确定性越小，包含的信息量也越少。
衡量数据间的相似性和差异性：
- 度量函数可以用来衡量不同数据集或数据点之间的相似性和差异性。例如，欧几里得距离、曼哈顿距离和余弦相似度等度量函数可以帮助我们比较数据点之间的距离，从而识别出相似的数据点或聚类。
评估数据的内在结构：
- 流形几何中的度量工具，如测地线距离和黎曼曲率，可以帮助我们评估数据在流形上的内在结构。通过分析数据的几何特征，我们可以揭示数据的复杂性和潜在模式，从而更好地理解数据的价值。
分析数据的拓扑特征：
- 拓扑数据分析（TDA）中的度量工具，如贝蒂数和持续同调群，可以帮助我们分析数据的拓扑特征。通过度量数据的拓扑复杂度，我们可以识别出数据中的全局结构和局部模式，从而更全面地评估数据的价值。
构建综合价值度量框架：
- 通过结合信息熵、流形几何和拓扑特征等多个维度的度量工具，我们可以构建一个综合的数据价值度量框架。这个框架可以同时考虑数据的信息量、几何结构和拓扑特征，从而提供一个全面、可计算和可解释的数据价值评估方法。

3.2 数据价值度量的基本原理

数据价值的度量本质上是对数据所携带信息价值的量化。这种量化需要考虑以下几个关键方面：

信息熵度量：数据集 $D$ 的信息熵 $H (D)$ 反映了数据的不确定性减少程度，可以作为数据价值的基础度量：

$H (D) = - i \sum p (x_{i}) lo g p (x_{i})$

其中 $p (x_{i})$ 是数据点 $x_{i}$ 的概率分布。
流形复杂度：数据在流形上的分布特征反映了数据的内在结构。设 $M$ 为数据流形，其复杂度可以通过以下指标度量：
- 流形维数 $d im (M)$
- 黎曼曲率 $R (M)$
- 测地线距离 $d_{g} (x, y)$
拓扑特征：数据的拓扑特征通过持续同调群来度量。设 $β_{k}$ 为第k个贝蒂数，则拓扑复杂度可表示为：

$C_{t o p} (D) = k = 0 \sum n β_{k} \cdot w_{k}$

其中 $w_{k}$ 是各维度的权重系数。

基于上述原理，我们可以构建数据价值的综合度量函数：

$V (D) = α_{1} V_{in f o} (D) + α_{2} V_{g eo m} (D) + α_{3} V_{t o p} (D)$

其中：

$V_{in f o} (D)$ 是基于信息熵的价值度量
$V_{g eo m} (D)$ 是基于流形几何的价值度量
$V_{t o p} (D)$ 是基于拓扑特征的价值度量
$α_{1}, α_{2}, α_{3}$ 是相应的权重系数

这个度量框架具有以下特点：

完备性：同时考虑了数据的信息量、几何结构和拓扑特征
可计算性：每个分量都有明确的计算方法
可解释性：度量结果具有清晰的物理意义
可扩展性：框架可以根据具体应用进行调整和扩展

度量的实践考虑

在实际应用中，数据价值的度量还需要考虑以下因素：

时效性：数据价值随时间衰减，可引入时间衰减函数： $V (D, t) = V (D) \cdot e^{- λ t}$
稀缺性：数据的稀缺程度影响其价值，可通过市场供需关系调整： $V_{ma r k e t} (D) = V (D) \cdot S (D)$ 其中 $S (D)$ 是稀缺性系数。
质量因素：数据质量通过准确性、完整性等指标评估： $V_{q u a l i t y} (D) = V (D) \cdot Q (D)$ 其中 $Q (D)$ 是质量评分。

通过这个多维度量框架，我们可以对数据价值进行科学、系统的评估，为数据资产定价和交易提供理论基础。。

3.3 度量在数据价值度量中的应用

接下来基于前面的讨论和建立的度量框架，来论述如何应用。我们将使用具体的数据类别实例分别来讨论：1）个人数据；2）企业数据；3）公共（政府）数据。

1. 个人数据

个人数据包括用户的行为数据、偏好数据、社交数据等。这些数据的价值度量可以通过以下几个方面来实现：

信息量：通过计算个人数据的信息熵来度量其信息量。例如，用户的浏览历史、购买记录等可以反映用户的兴趣和偏好，其信息熵越高，数据的价值越大。

以亚马逊、Netflix 和 Google 为实际实例，我们可以具体计算这些公司的个人数据价值。

亚马逊

亚马逊拥有大量的用户行为数据，包括浏览历史、购买记录、评论等。我们可以通过以下几个方面来计算这些数据的价值：

信息量：假设亚马逊某用户的浏览历史包含 $n$ 个页面，每个页面的访问概率为 $p_{i}$ ，则该用户浏览历史的信息熵为： $H = - i = 1 \sum n p_{i} lo g p_{i}$ 例如，若某用户浏览了 10 个页面，每个页面的访问概率均为 0.1，则信息熵为： $H = - 10 \times 0.1 lo g 0.1 = 1$
几何结构：通过流形学习方法，我们可以将用户的行为数据嵌入到一个低维流��中。例如，假设用户的行为数据可以嵌入到一个 3 维流形中，其维数和曲率可以度量数据的复杂性和价值。
拓扑特征：亚马逊用户的社交网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。例如，假设某用户的社交网络图有 5 个连通分量和 10 个环路，则其贝蒂数为： $β_{0} = 5, β_{1} = 10$

Netflix

Netflix 拥有大量的用户偏好数据，包括观看历史、评分、评论等。我们可以通过以下几个方面来计算这些数据的价值：

信息量：假设 Netflix 某用户的观看历史包含 $m$ 部电影，每部电影的观看概率为 $q_{i}$ ，则该用户观看历史的信息熵为： $H = - i = 1 \sum m q_{i} lo g q_{i}$ 例如，若某用户观看了 5 部电影，每部电影的观看概率均为 0.2，则信息熵为： $H = - 5 \times 0.2 lo g 0.2 = 0.464$ （注：此处仅举例演示，并未严格计算实际熵值。）
几何结构：通过流形学习方法，我们可以将用户的偏好数据嵌入到一个低维流形中。例如，假设用户的偏好数据可以嵌入到一个 2 维流形中，其维数和曲率可以度量数据的复杂性和价值。
拓扑特征：Netflix 用户的社交网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。例如，假设某用户的社交网络图有 3 个连通分量和 7 个环路，则其贝蒂数为： $β_{0} = 3, β_{1} = 7$

Google

Google 拥有大量的用户搜索数据、位置数据等。我们可以通过以下几个方面来计算这些数据的价值：

信息量：假设 Google 某用户的搜索历史包含 $k$ 个关键词，每个关键词的搜索概率为 $r_{i}$ ，则该用户搜索历史的信息熵为： $H = - i = 1 \sum k r_{i} lo g r_{i}$ 例如，若某用户搜索了 8 个关键词，每个关键词的搜索概率均为 0.125，则信息熵为： $H = - 8 \times 0.125 lo g 0.125 = 0.75$
几何结构：通过流形学习方法，我们可以将用户的搜索数据嵌入到一个低维流形中。例如，假设用户的搜索数据可以嵌入到一个 4 维流形中，其维数和曲率可以度量数据的复杂性和价值。
拓扑特征：Google 用户的社交网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。例如，假设某用户的社交网络图有 4 个连通分量和 9 个环路，则其贝蒂数为： $β_{0} = 4, β_{1} = 9$

通过这些具体的计算实例，我们可以看到，基于信息量、几何结构和拓扑特征的多维度量框架可以有效地应用于不同公司的个人数据，帮助我们科学、系统地评估数据价值。

实验以下Notebook展示了如何计算数据的信息熵、流形复杂度和拓扑特征：

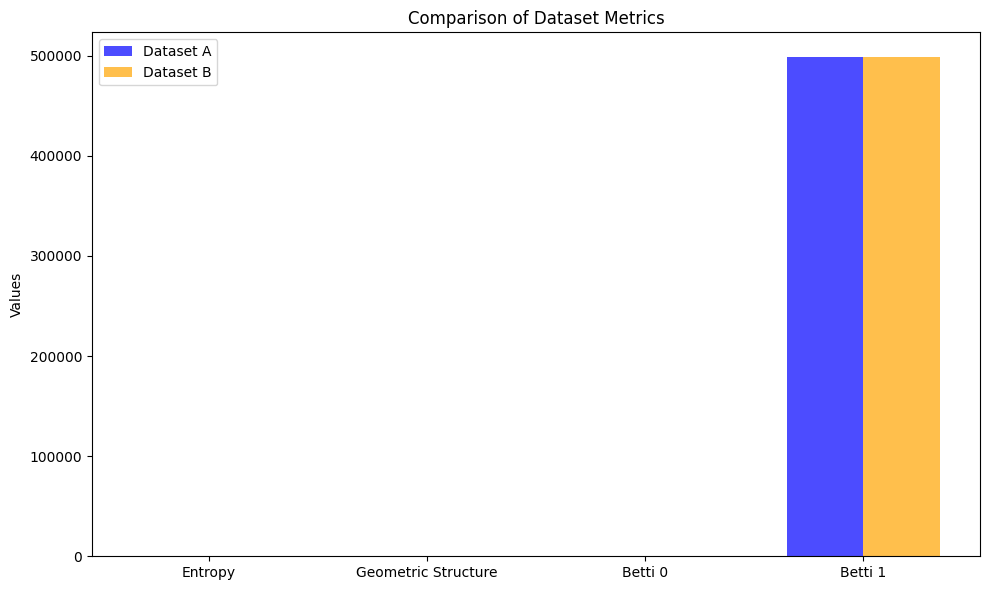
由于都是采用随机生成的数据，因此，可以看到数据的价值度量结果差异不大。数据价值度量结果

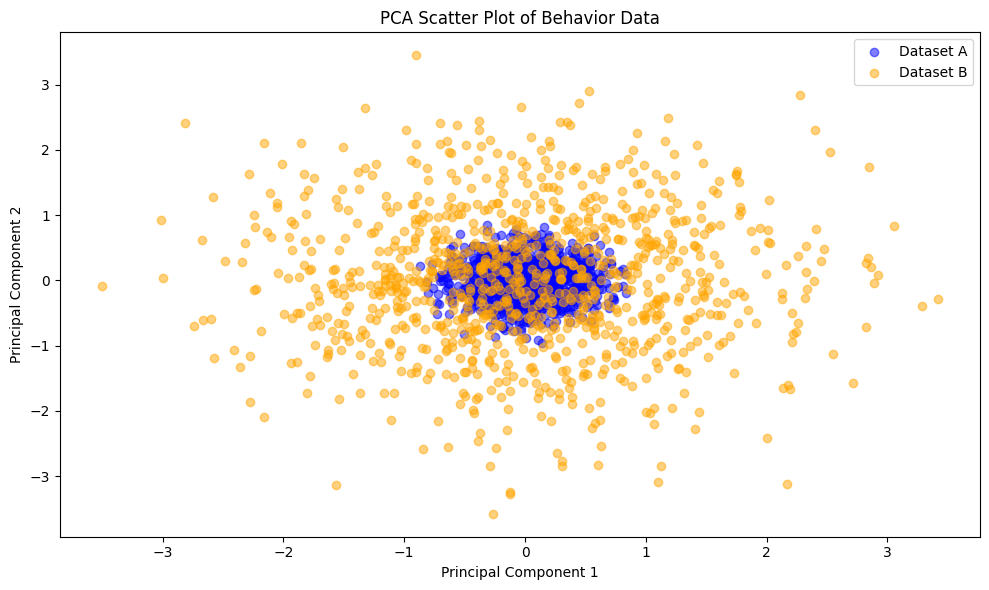
采用不同的分布，可以看到度量的差异。数据价值度量结果

2. 企业数据

企业数据包括生产数据、销售数据、客户数据等。这些数据的价值度量可以通过以下几个方面来实现：

信息量：通过计算企业数据的信息熵来度量其信息量。例如，企业的销售数据可以反映市场需求和销售趋势，其信息熵越高，数据的价值越大。
几何结构：企业数据的几何结构可以通过流形学习方法来分析。例如，生产数据可以嵌入到一个低维流形中，通过流形的维数和曲率来度量数据的复杂性和价值。
拓扑特征：企业数据的拓扑特征可以通过持续同调群来分析。例如，供应链网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。

实验以下Notebook展示了如何计算企业数据的信息熵、流形复杂度和拓扑特征：

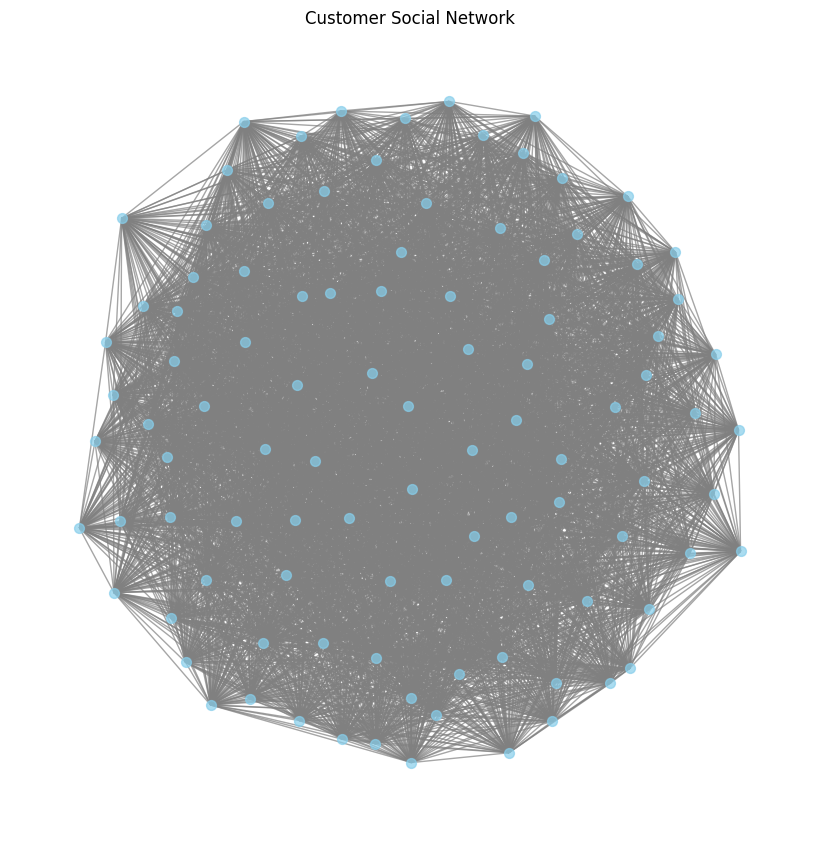
数据价值度量结果

3. 公共数据

公共数据包括气象数据、交通数据、人口数据等。这些数据的价值度量可以通过以下几个方面来实现：

信息量：通过计算公共数据的信息熵来度量其信息量。例如，气象数据可以反映天气变化和气候趋势，其信息熵越高，数据的价值越大。
几何结构：公共数据的几何结构可以通过流形学习方法来分析。例如，交通数据可以嵌入到一个低维流形中，通过流形的维数和曲率来度量数据的复杂性和价值。
拓扑特征：公共数据的拓扑特征可以通过持续同调群来分析。例如，人口分布可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。

实验以下Notebook展示了如何计算公共数据的信息熵、流形复杂度和拓扑特征：

实验数据显示如下：

Weather Data Entropy: 1.0861632625176211e-07
Traffic Data Entropy: 6.928893407164379
Weather Data Geometry: 0.42926119924422235
Traffic Data Geometry: 0.22809012569720633
Population Network Betti 0: 1
Population Network Betti 1: 3647

3.4 范畴论视角下的数据价值度量

在范畴论框架下，数据价值的度量可以通过以下几个方面来实现：

信息熵的范畴表示 设 $H : I \to R$ 是信息范畴上的熵函子，则数据的信息熵可表示为：

$H_{D} (D) = H (F (D))$

这个熵度量反映了数据转化为信息后的不确定性减少程度。

价值函子的可加性 对于数据范畴中的直和 $D_{1} \oplus D_{2}$ ，价值函子满足：

$V_{D} (D_{1} \oplus D_{2}) \geq V_{D} (D_{1}) + V_{D} (D_{2})$

这个不等式反映了数据组合可能产生的协同价值。

信息保持度 通过考察函子 $F$ 的保真度来评估数据价值：

$δ (D) = \frac{dim F ( D )}{dim D}$

其中 $dim$ 表示维数或信息��的某种度量。

范畴论与流形、拓扑构建的度量的联系与区别

在数据价值度量的研究中，范畴论、流形和拓扑构建提供了不同的视角和工具。它们之间既有联系也有区别。

联系

抽象数学框架：
- 范畴论、流形和拓扑构建都属于抽象数学的范畴，提供了统一的理论框架来描述和分析数据的结构和性质。
- 这些方法都强调数据的全局结构和关系，而不仅仅是局部特征。
信息的表示与转换：
- 在范畴论中，数据通过函子从一个范畴映射到另一个范畴，信息通过自然变换在不同的函子之间传递。
- 在流形和拓扑构建中，数据通过坐标图和同调群表示，信息通过不同尺度和视角下的拓扑特征来捕捉。
度量的多样性：
- 范畴论中的度量可以通过熵函子、价值函子和信息保持度来实现。
- 流形和拓扑构建中的度量可以通过Fisher信息度量、KL散度和持续同调群来实现。

区别

理论基础：
- 范畴论基于对象和态射的抽象结构，强调对象之间的关系和变换。
- 流形和拓扑构建基于几何和拓扑的概念，强调数据的空间结构和拓扑特征。
应用范围：
- 范畴论适用于广泛的数学和计算机科学领域，包括数据分析、编程语言和逻辑等。
- 流形和拓扑构建主要应用于几何、物理和高维数据分析等领域。
度量方法：
- 范畴论中的度量方法侧重于数据的变换和信息的传递，如熵度量和价值函子。
- 流形和拓扑构建中的度量方法侧重于数据的几何和拓扑特征，如Fisher信息度量和持续同调群。

范畴论与流形、拓扑构建在数据价值度量中提供了不同但互补的视角。范畴论强调数据的抽象关系和变换，而流形和拓扑构建则关注数据的几何和拓扑结构。通过结合这两种方法，我们可以更全面地理解和评估数据的价值。

实验以下Notebook展示了如何计算数据的信息熵、流形复杂度和拓扑特征：

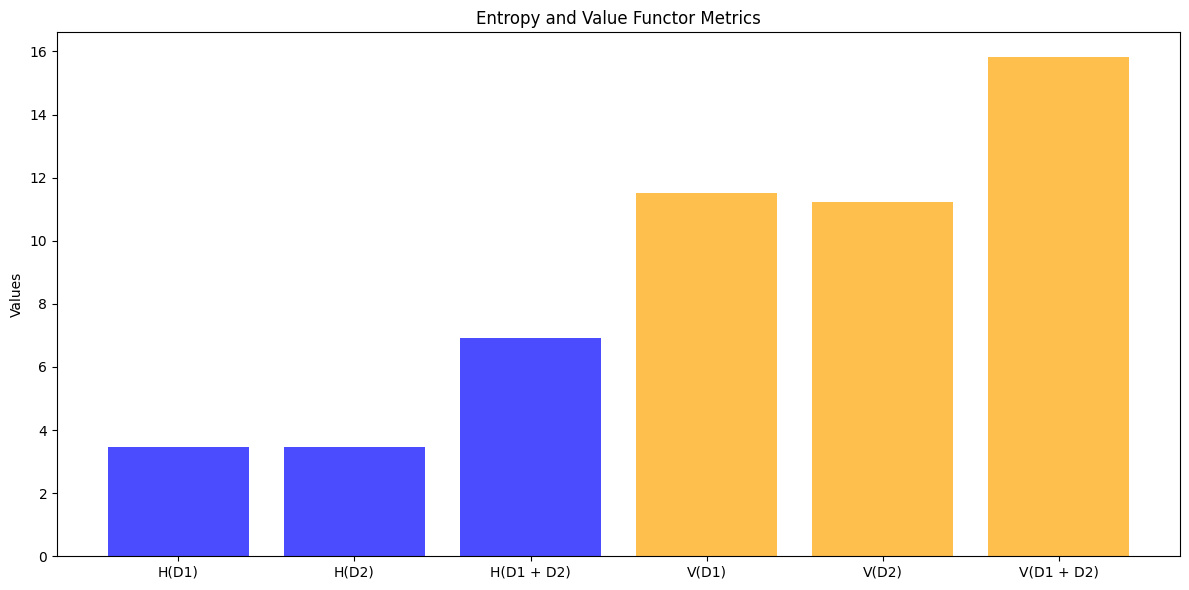
数据价值度量结果

通过实验，验证范畴论度量的三个方面：信息熵、价值函子的可加性和信息保持度，并通过图表直观展示结果。

实践意义

范畴论框架在数据价值研究中��有重要的实践意义。首先，它为数据价值评估提供了坚实的理论基础。通过范畴论的数学语言，我们不仅能够严格地定义和度量数据价值，还能深入理解数据价值的来源及其传递机制。这种理论框架为数据资产的科学定价提供了可靠的数学依据，使得数据价值评估从经验判断转向了理性分析。

其次，范畴论框架能够有效指导数据处理的优化。在这个框架下，我们可以将数据处理视为范畴间的函子映射，从而系统地设计最优的数据分析流程。这种理论指导不仅适用于数据清洗和特征提取等基础工作，还能帮助我们找到实现数据价值的最优路径。通过范畴论的视角，我们能够更好地理解和优化数据处理的每个环节，确保数据价值得到最大化的实现。

最后，范畴论框架为数据资产管理提供了系统的理论支撑。它不仅为数据资产的分类提供了科学的理论基础，还能指导数据资产组合的优化策略。特别是在评估数据资产的协同效应时，范畴论的工具能够帮助我们准确把握不同数据资产之间的关系和相互作用。这使得数据资产管理从单一资产的管理提升到了整体资产组合的优化层面，为数据经济时代的资产管理提供了新的思路和方法。

3.5 量化数据集价值的起点

在前面的章节中，我们详细介绍了多种度量方法，包括欧式距离、曼哈顿距离、切比雪夫距离、余弦相似度、马氏距离、汉明距离、黎曼度量和贝蒂数等。这些度量方法为我们提供了量化数据集特征的工具，使我们能够为任何一个数据集计算出一个“量”，作为数据价值定价的起点。

度量框架的普适性

多样性和灵活性：
- 度量框架的多样性和灵活性使得我们可以根据数据集的具体特征选择合适的度量方法。例如，对于高维数据集，我们可以选择马氏距离来考虑数据的协方差；对于字符串数据集，我们可以选择汉明距离来计算不同字符的个数。
- 这种多样性和灵活性确保了我们可以为任何类型的数据集找到合适的度量方法，从而计算出一个“量”。
统一的数学基础：
- 所有的度量方法都基于统一的数学基础，即度量空间的定义。
- 这种统一的数学基础确保了我们可以在不同的度量方法之间进行比较和转换，从而为数据集计算出一个一致的“量”。
度量学习的支持：
- 除了传统的度量方法，度量学习（Metric Learning）为我们提供了从数据中学习合适度量函数的工具。通过度量学习，我们可以根据数据集的具体特征和任务需求，学习到一个最优的度量函数。
- 度量学习的支持进一步增强了度量框架的普适性，使得我们可以为任何数据集计算出一个“量”。

计算“量”的过程

选择合适的度量方法：
- 根据数据集的具体特征和分析需求，选择合适的度量方法。例如，对于图像数据集，可以选择余弦相似度来衡量图像特征向量之间的相似性；对于时间序列数据集，可以选择动态时间规整（DTW）来计算时间序列之间的距离。
计算度量值：
- 选择合适的度量方法后，计算数据集中每对数据点之间的度量值。例如，对于欧式距离，可以计算每对数据点之间的直线距离；对于马氏距离，可以计算每对数据点之间的加权距离。
聚合度量值：
- 将计算得到的度量值进行聚合，得到数据集的整体度量值。例如，可以计算所有度量值的平均值、最大值或最小值，或者使用聚类算法将数据点分组，并计算每个聚类的中心点之间的距离。

数据价值定价的起点

通过上述过程，我们可以为任何一个数据集计算出一个“量”，这个“量”可以作为数据价值定价的起点。具体来说：

量化数据价值：
- 通过计算数据集的整体度量值，我们可以量化数据的相似性和差异性，从而为数据价值定价提供一个客观的基础。例如，度量值越大，数据集的多样性越高，潜在价值也越大。
评估数据质量：
- 度量值还可以用于评估数据的质量。例如，度量值越小，数据点之间的相似性越高，数据的冗余度越大，质量越低。通过评估数据质量，我们可以更准确地进行数据价值定价。
指导数据处理：
- 度量值还可以指导数据处理的优化。例如，通过分析度量值的分布，我们可以识别出数据集中的异常点和噪声，从而进行数据清洗和预处理，提高数据的质量和价值。

通过上述过程，我们可以为任何一个数据集计算出一个“量”，这个“量”可以作为数据价值定价的起点。

3.6 数据价值度量的数学证明

基于第二章对数据价值与信息价值关系的范畴论分析，我们可以严格证明为什么对数据集计算出的"量"可以作为数据价值定价的起点。

3.6.1 从范畴映射到数值映射

设 $D$ 为数据范畴， $I$ 为信息范畴， $F : D \to I$ 为从数据到信息的函子。根据前文分析，数据的价值源于其携带的信息。因此，对数据价值的度量实质上是寻找一个从数据范畴到实数的映射：

$V : D \to R$

这个映射需要满足以下性质：

函子性质保持：对于数据范畴中的态射 $f : D_{1} \to D_{2}$ ，有： $V (D_{2}) \geq V (D_{1})$ 这反映了数据处理不会增加数据的内在价值。
信息保持：存在信息范畴中的价值函数 $V_{I} : I \to R$ ，使得： $V (D) = V_{I} (F (D))$ 这保证了数据价值度量与信息价值度量的一致性。

3.6.2 价值度量的普遍构造

价值度量的构造可以通过如下步骤实现：

局部度量：对数据范畴中的每个对象 $D$ ，通过其局部特征定义基本度量： $V_{l oc a l} (D) = i \sum α_{i} m_{i} (D)$ 其中 $m_{i}$ 是各种局部度量（如信息熵、流形维数等）， $α_{i}$ 是权重系数。
全局修正：考虑数据在整个范畴中的位置： $V_{g l o ba l} (D) = V_{l oc a l} (D) \cdot γ (D)$ 其中 $γ (D)$ 是反映数据全局特征的修正因子。
价值函数的泛性质：最终的价值函数应满足泛性质，即对于任意其他满足基本性质的度量函数 $W$ ，存在唯一的变换 $ϕ$ ，使得： $W (D) = ϕ (V (D))$

3.6.3 数据价值度量的合理性

这种度量构造的理论合理性可以通过如下严格的数学证明来验证：

数学一致性：通过函子 $F$ 建立的数据价值与信息价值之间的对应关系必须保持一致： $V (D) = V_{I} (F (D)) = \int_{M} ρ (F (D)) d μ$ 这个等式保证了我们的度量方法与信息论的基本原理相符。
稳定性保证：一个合理的度量方法应当对数据的微小变化具有稳定性。即对数据的小扰动 $ϵ$ ，价值变化应当有界： $∣ V (D + ϵ) - V (D) ∣ \leq K ∥ ϵ ∥$ 这保证了度量结果不会因为数据的细微噪声而产生剧烈波动。
可加性原理：对于独立的数据集，其价值应满足近似可加性： $V (D_{1} \cup D_{2}) \approx V (D_{1}) + V (D_{2}) + I (D_{1}; D_{2})$ 其中 $I (D_{1}; D_{2})$ 表示两个数据集之间的信息关联度。这符合数据价值的直观认识。
单调性：数据处理过程不应增加数据的内在价值： $若 D_{1} f D_{2}, 则 V (D_{2}) \leq V (D_{1})$ 这反映了信息处理不增原理。

（注：此处的数据处理过程，限定为不引入额外外部信息的纯数据内部处理过程，即只做数据内部变换，不额外合并新的数据源。这样才能严格保证单调性。若引入“外部信息”或“数据融合”，则价值有可能增加。）
可计算性：理论必须能转化为具体的计算方法：
- 有明确的计算步骤
- 计算复杂度在可接受范围内
- 结果具有数值稳定性

基于前文建立的理论框架，我们可以深入理解为什么经过合理构造的"量"能够作为数据价值定价的基础。这个问题的核心在于我们建立的数学框架与数据价值的本质特征之间存在严格的对应关系。

首先，我们构造的度量方法严格保持了数据到信息的函子映射结构。这意味着当数据通过某种处理或转换时，其价值的变化是可追踪和可预测的。通过函子的性质，我们能够确保数据处理过程中的价值传递符合信息论的基本原理。这种结构保持性为数据价值评估提供了理论保障，使得我们能够在数据流转和处理的各个环节准确追踪其价值变化。

其次，我们的度量方法满足了一系列关键的数学性质，包括稳定性、单调性和可加性。稳定性保证了对数据的微小扰动不会导致价值评估的剧烈波动；单调性确保了数据处理不会凭空产生价值；可加性则反映了数据组合的协同效应。这些数学性质共同构成了一个完整的理论框架，使得我们的价值度量方法在数学上是严格自洽的。

更重要的是，这个理论框架提供了一种系统的构造方法，能够从局部特征出发，通过严格的数学推导，最终得到反映数据整体价值的全局度量。这种从局部到全局的构造过程不是简单的叠加，而是考虑了数据内部的关联结构和整体特征。通过这种方法，我们能够捕捉到数据价值的多个层面，从而得到更全面和准确的评估结果。

最后，我们的理论具有普遍性和稳定性这两个关键特征。普遍性意味着这个理论框架可以应用于各种类型的数据和不同的应用场景；稳定性则确保了理论在实际应用中的可靠性。这两个特征使得我们的理论既有足够的适应性来处理各种实际问题，又能保持必要的稳健性以产生可靠的结果。

3.7 数据价值度量的未来展望

在数据价值度量研究中，我们目前主要运用了三种数学工具：数据流形、数据拓扑和范畴论。这些工具各自关注数据价值的不同方面，形成了互补的分析框架。

数据流形和数据拓扑提供了定量分析的基础。通过计算流形的几何特征（如维数、曲率）和拓扑不变量（如贝蒂数、持续同调），我们能够对数据的结构特征进行精确的数值度量。这些可计算的指标为数据资产定价提供了客观的量化依据。

范畴论则从更抽象的层面提供了定性分析的框架。它通过研究数据范畴之间的函子关系和自然变换，揭示了数据价值的传递机制和普遍性质。这种理论分析虽然不直接给出具体的数值，但为我们理解数据价值的本质提供了深刻的洞察。

未来数据价值度量研究的关键方向是：

定量与定性的统一：
- 建立范畴论框架下的数值计算方法
- 将拓扑不变量与函子映射关联起来
- 发展基于范畴论的数值优化算法
多尺度分析的融合：
- 将局部几何特征与全局拓扑性质统一起来
- 建立跨尺度的价值传递机制
- 发展多尺度数据价值评估方法
动态价值评估：
- 研究数据价值随时间演化的规律
- 建立数据价值的动态预测模型
- 发展实时数据价值评估系统

数据资产定价导论